25 zaujímavých faktov o matematike
- Musíme uznať, že aj keď matematika je asi najnenávidenejší predmet zo všetkých, má naozaj svoje čaro. Bez nej by totiž neexistovali mnohé technológie.

- Musíme uznať, že aj keď matematika je asi najnenávidenejší predmet zo všetkých, má naozaj svoje čaro. Bez nej by totiž neexistovali mnohé technológie.
Hairy Ball Theorem
“Hypotéza chlpatej gule” algebrickej topológie uvádza, že neexistuje žiadne nenulové kontinuálne tangenciálne vektorové pole na viacrozmernej guli.
V jednoduchosti to znamená, že nemôžete usporiadať všetky chlpy na tenisovej loptičke tým istým smerom bez toho, aby ste dostali takzvaný “cowlick”.
6 týždňov sa rovná presne 10! (faktoriál) sekúnd
Poďme si to vysvetliť: v šiestich týždňoch máte 1 sekundu x 60 x 60 x 24 x 7 x 6. Z tohto vzorca sme dostali čísla 1, 7 a 6. Teraz potrebujeme iba ten zvyšok.
60 = 2 x 3 x 10
60 = 5 x 4 x 3
24 = 8 x 3
Týmto rozložením sme ale dostali dve trojky navyše. Tie však stačí navzájom vynásobiť: 3×3=9. Teraz už máme všetko čo potrebujeme: 1x2x3x4x5x6x7x8x9x10 čo je 10! sekúnd.
Keď nikto nič negarantuje
Toto je skôr štatistický fakt, ale pokiaľ existuje šanca 1 z x a opakovaní je rovnako x, pri veľkých číslach nad 50, je pravdepodobnosť iba okolo 63%.
1-(1-1/x)^x
Napríklad: Ak existuje šanca 1 z 10 000, že vás zasiahne meteorit, ak pôjdete von a vy pôjdete von 10 000-krát, pravdepodobnosť, že vás zasiahne meteorit je 63%. Ak existuje šanca 1 z milióna, že vyhráte lotériu a vy si kúpite milión losov, máte iba 63% pravdepodobnosť na úspech.
Delenie sedmičkou
Pokiaľ vydelíte akékoľvek číslo číslom 7 a výsledok nebude celé číslo, za desatinnou čiarkou dostanete rad čísel 142857.
1/7 = 0.142857142857
3/7 = 0.428571428571
2/7 = 0.285714285714
6/7 = 0.857142857142
4/7 = 0.571428571428
5/7 = 0.714285714285
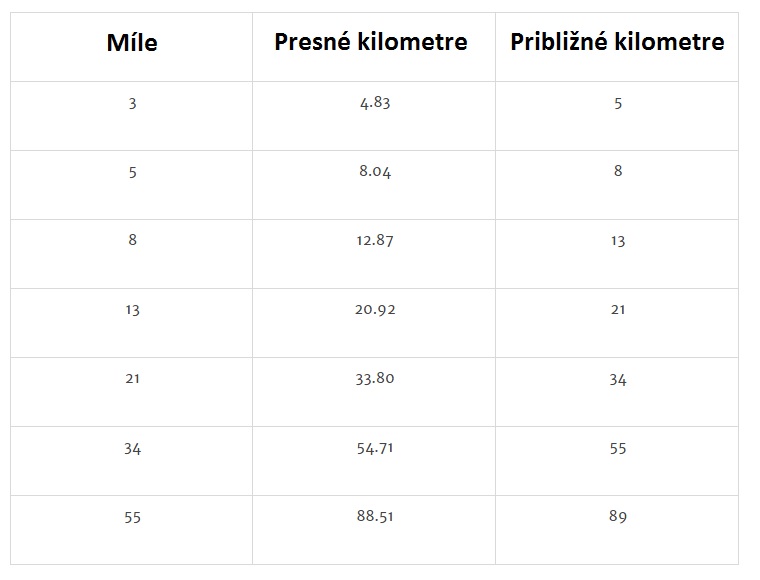
Fibonnaci v mílach a kilometroch
Na takmer dokonalý prevod míl na kilometre môže poslúžiť Fibonnaciho postupnosť
1 1 2 3 5 8 13 21 34 55 89 ….
Preskočte pár prvých čísel a možete sa činiť…
img: via kickassfacts.com
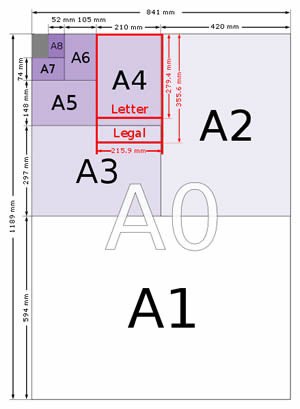
Kúzelná A4
Medzinárodné formáty papiera (ako je A4) používajú pomer strán 1:√2. Pokiaľ by ste papier takéhoto formátu priečne prerezali na polovicu, dostali by ste rovnaký pomer.
img: via kickassfacts.com
Balíček kariet
Existuje 52! (faktoriál) spôsobov, ako zamiešať balíček kariet alebo…
80658175170943878571660636856403766975289505440883277824000000000000 spôsobov.
Ako veľké je toto číslo?
Najskôr si vyberte svoj obľúbený bod na rovníku. Teraz miešajte balíček kariet každú sekundu. Chystáte sa kráčať pozdĺž rovníka okolo Zeme, ale budete kráčať veľmi pomaly. Každú miliardu rokov spravíte iba jeden krok. Po tom, čo obídete celú Zem dookola, vyberiete jednu kvapku vody z Tichého oceána.
Teraz robte rovnakú vec stále dookola: kráčajte okolo Zeme rýchlosťou jedného kroku za miliardu rokov a vyberajte kvapku vody z Tichého oceána vždy, keď Zem obídete dookola. Pokračujte až vyprázdnite celý oceán. Keď ho vyprázdnite, položte na zem list papiera. Teraz naplňte oceán späť a začnite celý proces odznovu, pričom pridáte list papiera vždy, keď vyprázdnite oceán.
Pokračujte, až kým hora papiera nedosiahne až k Slnku. Ak sa pozorne pozriete na stopky, zistíte, že prvé tri cifry sa ani nezmenili. Stále vám ostáva 8.063e67 sekúnd (jedna sekunda sa rovná jednému zamiešaniu balíčka). Jedna astronomická jednotka (vzdialenosť od Zeme k Slnku) je 149 597 870 692 kilometrov. Takže strhnite stĺp papiera a začnite odznova. Dokopy ešte 1000-krát. Nanešťastie, stále to nebude stačiť. Stále budete mať 5.385e67 sekúnd. Zatiaľ ste iba v jednej tretine svojej cesty.
Počítajte na prstoch do 1023
Používaním binárnej sústavy môžete na jednej ruke narátať do 31 a na dvoch do 1023. (Zdroj)
The Monty Hall problem
Predstavte si, že ste na súťaži, kde sa nachádzajú troje dvere a za jednými je hlavná výhra. Vy máte za úlohu vybrať jedny z dverí. Keď ich vyberiete (napr. dvere číslo 1), moderátor súťaže otvorí jedny zo zostávajúcich dvoch dverí, kde nič nie je (napr. dvere číslo 2). Následne sa vás opýta, či chcete zmeniť váš výber a zvoliť druhé neotvorené dvere, ktoré ste predtým neoznačili (napr. dvere číslo 3). Zmenili by ste svoj výber?
Štatisticky by ste ho zmeniť mali! Existuje totiž 66,6% šanca, že za dverami číslo 3 sa nachádza rozprávková výhra. Pre dvere, ktoré ste zvolili ako prvé, je táto pravdepodobnosť iba 33,3%. Niekto by mohol argumentovať, že je to 50/50, ale nie je to tak.
Vysvetlenie: Na začiatku majú každé dvere 33,3% pravdepodobnosť na výhru. Ak zvolíte dvere číslo 1, existuje tak 33,3% pravdepodobnosť, že výhra sa nachádza za týmito dverami, ale 66,6% pravdepodobnosť, že výhra sa nachádza sa dverami číslo 2 alebo 3. Po tom, čo moderátor otvorí jedny z nevýherných dverí, pravdepodobnosť pre dvojicu dverí 2 a 3 zostáva stále 66,6%, ale už sa tam budú nachádzať iba jedny dvere.
Dokonalé číslo 73
Číslo 73 je 21. prvočíslo. Jeho zrkadlový obraz je 37, čo je 12. prvočíslo, čoho zrkadlový obraz je 21, čo je výsledok násobenia 7 a 3. V binárnej sústave je číslo 73 palindróm – 1001001, čo sa číta odzadu úplne rovnako. Ak k číslu 73 a aj jeho zrkadlovému obrazu – 37 – pripočítate 100, stále budete mať prvočísla (173 a 137).
Pokiaľ si vezmete číslo 73 a jeho zrkadlový obraz zväčšený o 100 (137) a vynásobíte ich navzájom, dostanete číslo 10 001. To môžete použiť na jeden matematický trik: Myslite si hocijaké štvorciferné číslo. Vynásobte ho 73, potom ho vynásobte 137. Dostanete vaše číslo napísané dvakrát za sebou.

Drahý náter
Existujú 3D objekty, ktoré majú nekonečný povrch, ale konečný objem. Napríklad Gabrielov roh, ktorý je na obrázku vyššie. Môžete ho naplniť farbou, ale nikdy nebudete mať dostatok na jeho natretie. Roh sa totiž predlžuje do nekonečna, čiže povrch nikdy nekončí. Jediný dôvod, prečo môžete roh naplniť farbou je ten, že ako sa predlžuje, stáva sa veľmi úzkym. Tým pádom objem dosahuje konečné číslo.
The Banach-Tarski Paradox
Hypotéza hovorí o tom, že môžete rozrezať guľu na kúsky a znovu z nich postaviť dve gule, ktoré sú rovnaké ako tá pôvodná.
Potato paradox
Miško domov donesie 100 kíl zemiakov, ktoré obsahujú 99% vody. Nechá ich cez noc vonku, vďaka čomu podiel vody klesne na 98%. Akú hmotnosť majú zemiaky teraz? Možno vás prekvapíme odpoveďou, ale je to 50 kíl.
Hmotnosť vody: 99% = 99 kg
Zvyšná hmotnosť: 1% = 1 kg
Keďže nemôžete zrazu získať viacej “nevodnej” hmotnosti, zvyšná hmotnosť bude stále rovnaká:
Zvyšná hmotnosť: 2% = 1 kg
Nová hmotnosť vody: 98% = 49 kg
49+1 = Nová celková hmotnosť = 50 kg
Birthday Problem
Pokiaľ zozbierate 23 úplne náhodných ľudí, existuje 50% pravdepodobnosť, že dvaja z nich budú mať rovnaký deň narodenia (nie rok).
Naozaj hrubý papier
Pokiaľ by ste zložili papier na polovicu 107-krát, jeho hrúbka by bola väčšia než šírka pozorovateľného vesmíru.
Nejaké tie míľniky: 23 zložení – 1 km, 42 zložení – vzdialenosť k Mesiacu, 53 zložení – vzdialenosť k Slnku.

Múdri ľudia z Futuramy
Matematické vzorce použité v jednom z dielov Futuramy (s prehadzovaním tiel) sú súčasťou skutočnej hypotézy, ktorú vytvoril scenárista Futurami Ken Keeler, ktorý má PhD.z aplikovanej matematiky. (Zdroj)
Googolplex
Vo vesmíre neexistuje dostatok priestoru, aby sme mohli vypísať celé číslo googolplex. Aj keby bola každá nula veľkosti atómu.
Babylončania
Staroveký Babylončania používali matematiku založenú na 60, nie na 10 ako my v súčasnosti. Z tohto dôvodu má minúta 60 sekúnd a kruh 360 stupňov. Zdroj
Keď si v matike naozaj dobrý
Pred viac ako 2000 rokmi, Eratosthenes vypočítal obvod Zeme iba vďaka primitívnej matematike. A dokonca pri tom ani neopustil Egypt! Jeho výpočty boli s presnosťou 2%. (Zdroj)
Nekonečno alebo konečno?
1 + 1/2 + 1/4 + 1/8 + 1/16 + … sa rovná 2, ale…
1 + 1/2 + 1/3 + 1/4 + 1/5 + … sa rovná nekonečno.

Fejkový Pytagoras
V skutočnosti neexistuje žiaden záznam o tom, že Pytagoras niekedy pracoval na tejto teórii alebo potvrdil Pytagorovu vetu. Dokonca neexistuje ani žiaden záznam, že by riešil čo i len nejaký matematický problém. (Zdroj)
Zbytočná presnosť
Falošne pozitívny paradox opisuje situáciu, kde sú veľmi presné testy zbytočné, pokiaľ podmienka testovania je dostatočne zriedkavá.
Príklad: Pokiaľ 10 ľudia v 20-miliónovom meste sú “zlí” a monitorovací program ich rozpoznáva s 99% presnosťou, potom 99,995% pozitívnych výsledkov bude v skutočnosti falošných. (Zdroj)
Priateľov ako maku
Na základe Paradoxu priateľstiev (“Friendship Paradox”), vaši priatelia majú viac priateľov, než vy. (Zdroj)
Like a boss
Dlho sa verilo, že číslo (2^67 -1) je prvočíslo, až kým to nevyvrátil matematik Frank Nelson Cole. Týmto problémom sa zaoberal 3 roky každú nedeľu.
Na matematickej konferencii v roku 1903, počas prednášky, ktorú mal predniesť, prikročil k tabuli priamo pred plnú sálu jeho kolegov matematikov. V úplnom tichu napísal na tabuľu 147 573 952 589 676 412 927, čo sa rovná (2^67 -1). Potom sa presunul k druhej strane tabule, kde napísal 193 707 721 x 761 838 257 287. Následne ručne spravil celý výpočet, čoho výsledkom bolo číslo rovnaké ako (2^67 -1).
Položil kriedu na stôl a v úplnom tichu sa vrátil na svoje miesto, zatiaľ čo prijímal standing ovation od publika. (Zdroj)
Hora textu
Podľa Zipfovho pravidla, v dostatočne veľkej vzorke textu z akéhokoľvek jazyka, najfrekventovanejšie slovo sa bude objavovať dvakrát viac ako druhé najfrekventovanejšie, trikrát viac ako tretie, štyrikrát viac ako štvrté a tak ďalej.. (Zdroj)
zdroj: vedelisteze.sk, zdroj titulnej fotografie: /zsido.comkickassfacts.com